



Next: Modifications to the Viscous
Up: Review of Inhomogeneous Registration
Previous: Combination Multiquadric Spline (C-MTQ)
Elastic Registration with Variable Elasticity
Davatzikos [4] presents an elastic registration model applied to images of the head where the elasticity parameters vary spatially within the image. The deformation is driven by distances between parametrically-defined pre-segmented cortical and ventricular surfaces in the source and target, and also incorporates a pre-strained elasticity term. The latter allows for voluntary growth in specified image areas, for example to model the growth of a tumour.
First the brain tissue is segmented from the images and a deformable surface is applied to the source and target brain volumes, giving for each a parametric description of the shape of the outer cortical surface.
At each point on the ventricular surface in the deforming source, a force is computed from the distance to the nearest point on the boundary of the target ventricular surface, weighted by the scalar product of outward normals at these points. These ventricular forces together with cortical forces derived from matching cortical surfaces by curvature measures provide a total external driving force field 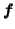 which is supplied to the variable-elasticity equation:
which is supplied to the variable-elasticity equation:
The first bracketed term is the regularisation between driving forces 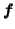 and the elasticity constraints on the displacements vector
and the elasticity constraints on the displacements vector
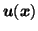 .
The second contains gradients in the elasticity parameters
.
The second contains gradients in the elasticity parameters 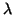 and
and 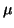 ,
allowing variation in the elasticity field.
The third term contains gradients in a parameter
,
allowing variation in the elasticity field.
The third term contains gradients in a parameter 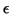 determining an additional strain tensor
determining an additional strain tensor
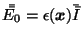 which forces extra expansion or contraction in pre-selected regions. Hence the algorithm also contains inhomogeneities in activity, or data influence.
which forces extra expansion or contraction in pre-selected regions. Hence the algorithm also contains inhomogeneities in activity, or data influence.




Next: Modifications to the Viscous
Up: Review of Inhomogeneous Registration
Previous: Combination Multiquadric Spline (C-MTQ)
Hava LESTER
1999-03-24
![]() which is supplied to the variable-elasticity equation:
which is supplied to the variable-elasticity equation: