Sad, but True, or- The Special Cases

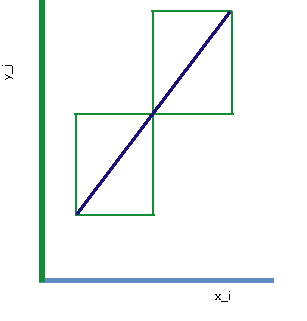
The theory is almost perfect, but, there are some rules as a confirmation of the initial hypothesis, for which the previously shown won't work. If we have the same linear relationship between features in both classes, given with x_j=k*x_i+a, then we are reaching the minimum level of informativeness of joint, correlated features on the boundaries of [-1,1] interval, depending on the sign of k.

1. For k>0, we have the following equalities:

J_j=J_i=I (23)

assuming that we denoted the common divergence with I

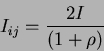$$J_{ij}=\frac{2J}{(1+\rho)}$$ (24)

In this case we have $\lim_{\rho\to 1}J_{ij}=I$. Thus, the point of maximum redundancy is shifted to the boundary point $\rho=\sqrt{J/J}=1$, and we have that the informativeness of two joint features drops to its minimum value, equal to the informativeness of individual feature (either of them, since they are equal). This special case is depicted in the figure above, and is represented with degenerate scattering ellipses which consist of two segments of the same line.

2. For k<0, maximum level of redundancy is shifted to the left to the point $\rho=-1$, where we fall down to the minimum level of informativeness (easily shown through the value of divergence), with:

I_j=I_i=I (25)

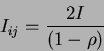$$I_{ij}=\frac{2I}{(1-\rho)}$$ (26)

$$\lim_{\rho\to 1}I_{ij}=I$$ (27)

Conclusion like the following could be derived:

Generally, the joint informativeness of features that are strongly stochastically or linearly related increases significantly comparing to the individual informativeness that we get from each of the features taken separately. This way, even features with very poor discriminating power, but mutually strongly correlated can constitute highly informative system. There are exemptions, though: in special cases of same linear regressions of features in both classes, joint informativeness decreases on the boundaries of correlation coefficient interval [-1,1]. It could be less than the sum of the informativeness of individual features, and equals the informativeness of individual feature on the very boundary of the given interval for $\rho$.

These are very important conclusions, since, in pattern recognition we are searching for the best solution, that is to find the minimum set of features with maximum informativeness of joint features.

<< >>