Assumptions and Criteria of Goodness of LDF Performance

Assumptions:

• we are classifying the specimens into only two classes
• features are represented with d dimensional vectors that follow a Multivariate Normal Gaussian Distribution, with the same covariance matrix in each class
• variates that constitute feature vectors are scaled in a sense that they reach the unit standard deviation in each of the classes, and that they have zero mean in class one and some positive value $\mu_i$, i=1,...,d, in class two
• training sequences were large enough so that $\mu_i$, as well as the correlation coefficient $\rho_{ij}$ are known with negligible error
• criterion of LDF performance is the probability of misclassification (find out about limitations of simple distance classifiers here )

Let feature vector X be d-dimensional ( X=[x₁,x₂,...,x_d]), and let its components be such that for each x_i, i=1,...,d mean values follow the above assumptions.

Criterion of goodness of the individual discriminator x_i is given through the probability of misclassification, that is:

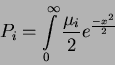$$P_i=\int\limits_0^{\infty}\frac{\mu_i}{2}e^{\frac{-x^2}{2}}$$ (28)

Hence, with all given above we can actually rank our discriminators with respect to their individual power. Table 1. gives the overview of the relation between $P_i, \mu_i,\mu_i^2$, for certain values.

Pi %	45	40	35	30	25	20	15	10	5	1
$\mu_i$	.251	.507	.771	1.049	1.349	1.683	2.073	2.563	3.290	4.653
$\mu_i^2$	.063	.257	.549	1.110	1.820	2.833	4.296	6.569	10.82	21.65

Looking at the given table, having the high accuracy of classification as a target, we can deduce that variates with P_i of 40% or more would be considered as poor variates.

<< >>