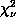5.3.2 Real Scans

Table 5.2 gives the results from the real scan studies with the brain phantom for over registrations. Note that the mean of the errors are non-zero. The mean of the errors from the point simulations are zero because of the exact knowledge of the true or correct registration - there were no systematic errors. The non-zero mean values from the real scans reflect the systematic error in the finite localisation of the fiducial positions. This does not effect the specification of the error in terms of and which characterise the uncertainty of the distributions - irrespective of systematic error in the bases for true registrations. Note that in the y dimension is larger than for the x dimension. x &y form the transaxial slices in this study. The y dimension corresponds to the largest dimension of the brain in the anterior-posterior orientation. The greater resolution capabilities of SPECT in the tangential direction as a source moves radially away from the axis of rotation gives rise to this asymmetry. The larger dimension of the brain through y implies that the resolution in the left-right orientation, through x, will be better and therefore reduce homology errors in that ordinate. through z, in the inferior-superior orientation, is similarly larger than through x &y because the resolution is poorest from lack of axial apodization.

From the point simulations, the radii of the configurations in each plane were expected to affect about the respective axes. Since the transaxial slices are generally largest in dimension, the disperse points in that plane defined the greatest spread or largest r. For a centered system, this explains why is smallest about the z axis, in the transaxial plane. Similarly, is largest in the coronal plane because of the smaller dispersion of homologous points about the imaginary y axis passing through the centroid. The values calculated for the test of the normal distribution of the translation and rotation errors are all reasonably close to unity. The deviations from the predicted Gaussian spread may thus be deemed acceptable for the respective because they yield integral probabilities, P, in the range such that the null hypothesis may not be rejected. The quotation of and thus allows the statement of the magnitude of the error with very large probability - approaching very near 1 from the integral probability of the underlying Normal distribution. The analytical evaluation of the integral of the Gaussian function is very complex in practice, but numerical techniques are used to evaluate the integral within yield an integral probability of 99.7 %[Bev69]. Using the resolution of the SPECT system quoted in table 5.1 as an approximation for , the known number of points used, m, and knowledge of the approximate dimension of the phantom (radii of about 9 cm through y, 7 cm through x, and 6.5 cm through z) to specify the spread of the configuration, the results from real scan studies correspond very well with those predicted by the point simulations within the standard deviation of the simulation data from the fit. For of about 10 mm from table 5.1, about the inferior-superior axis may seem a bit low. This is acceptable because of the radial dimension in the transaxial plane and the number of samples considered. The corresponding standard deviation of the differences between the simulation data and the fit is about (see figure 5.8 for shells and figure 5.11). With these considerations, the results about the other axes and the difference in the magnitude of between axes are shown to be predicted approximately by the results from the point simulation studies.