LDF with two variates -The effect of correlation

Let x₁ denote either a variate or a computed discriminant function with distance $\mu_{i1}$, and let x₂ be the new variate to be added to the first one, or to some already constructed LDF, at which we can look as at an variate itself. Signs of correlations are of crucial importance, and we will assume that the positive correlation coefficients mean that the intra-class correlation has the same sign as the correlation between the means of two classes.

Usually, in cases of natural applications positive correlations are more frequent than negative, because we commonly have different kinds of tests which make categorization either into two simple classes (yes-no, pass-fail, etc.), where most often the ''yes'' class has higher score, and hence, shows positive distance given by its mean value in the second class, $\mu_i$. That gives rise to positive correlation between classes. Also, one good performance accompanies another, thus, the intra-class correlations are positive as well. In spite of being rare, negative correlations can occur (Iris example of Fisher, 1936). But, how to actually calculate the increase in squared distance due to inclusion of the new variate x₂? Let's try with the following 'trick': variate $(x_2-\rho x_1)$ is independent of x₁ and has the distance between classes $\mu_2-\mu_1=\mu_2$-$\mu_2-\mu_1=\mu_2$$\mu_2-\mu_1=\mu_2$, and variance $1-\rho^2$. Knowing this, it is easy to see that the squared distance increases by the amount:

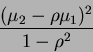$$\frac{(\mu_2-\rho \mu_1)^2}{1-\rho^2}$$ (30)

At the beginning of this section we have assumed that variates that are to be examined (whether to include them into LDF or not) show ''poor''performance as discriminators. For a given ''new'' discriminant x₂ the distance it preserves between classes is just a fraction of the established discriminator's distance- in other words: $\mu_{2}=f\mu_1$, where f is in the [0,1] interval.

We can play further and express the increase of original distance as a fraction of itself:

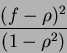$$\frac{(f-\rho)^2}{(1-\rho^2)}$$ (31)

For $\rho=0$ the increase in distance is reduced to f². Thus, correlation is helpful if it is satisfied:

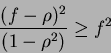$$\frac{(f-\rho)^2}{(1-\rho^2)}\ge f^2$$ (32)

Conclusions:

• Any NEGATIVE correlation is helpful. For $\rho\rightarrow -1$ there is no mathematical limit on the increase of squared distance. That is exactly the reason that we cannot really find any mathematical rule on how to predict joint discriminating power based on the knowledge of the individual discriminators.
• Positive correlation is useful only if it is high enough ( $\rho \ge \frac{2f}{1+f^2}$). For values of f = 0.7, 0.5, and 0.3, $\rho$ should exceed 0.94, 0.8, and 0.55, respectively.

For the positive correlations, we can further conclude that if we are to take a new feature with equal discriminating power (f=1), then all positive correlations are harmful; and for f=0, which means that the new feature has no discriminating power then all positive correlations are helpful (as well as negative).

If we want, by introducing a new discriminant, to obtain a significant increase of the goodness of overall LDF, meaning- the increase of its discriminating power- then the new feature (discriminator, or covariate) has to bring with itself a high level of correlation with the old feature or overall discriminator. Here are some examples:

• If $\mu_1=1.049$, giving the error rate of 30% then we need corr.coef.=0.63 in order to reduce the error rate to 25%, and corr.coef.=0.78 to lower down the error rate to 20%.
• With same distance $\mu_1$ and the initial error rate of 10% we need correlation coefficients equal to 0.6 and 0.78 in order to obtain error rate of 5%, or just 2%, respectevely.

And, again The Special Case, which occurs if we have the same linear regression of x₂ on x₁, in both classes. As we have seen before, for this constellation of variates, the error increases as $\mid\rho\mid\to 1$.

If all variates have linear regressions on a set of k variates, these k variates determine an upper limit that can be attained by the squared distance, no matter how many variates are included in the discriminant. It is important to notice that regressions must be THE SAME IN BOTH CLASSES.

<< >>