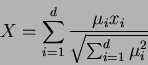 |
(29) |
For d independent variates, the best combined discriminant is given by:
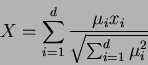 |
(29) |
where X is scaled so that it has unit standard deviation. Distance for X is given by
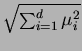 .
.
This way we can calculate the probability of misclassification for d-dimensional feature vector. Simply find the distance function at some point Xk, and decide for class one if it less then
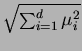 ,
otherwise decide for class two. In extension we can write
,
otherwise decide for class two. In extension we can write
![]() ,
because the effect of using m independent variates with distances
,
because the effect of using m independent variates with distances ![]() is the same as if we used one variate with distance
is the same as if we used one variate with distance ![]()
Going back to table 1, we can conclude that a single variate (discriminator in other words) with a 1% error rate is worth 2 variates with a 5% error rate, over 7 variates with 20% error rate, 20 variates with 30% error rate, etc.
But, this is the moment where we can use our conclusions from previous sections. Here it comes again- the reason why we have gathered, the sparkling theory that goes beyond common understanding of information flow, beyond common ability of comprehension...
What if variates were mutually correlated?
It would be nice if we finally discover who was the first...
Well, here they are- Cochran and Bliss. They have shown (53 years ago!) that a discriminant (to which they refer as to covariate) with no dicriminating power
(![]() )
when used alone, may greatly reduce the error rate under the assumption that it is highly correlated with a discriminant that has been constructed without that particular covariate.
)
when used alone, may greatly reduce the error rate under the assumption that it is highly correlated with a discriminant that has been constructed without that particular covariate.
Though we have already mentioned the old discriminators' rule, let's write it down again, with just a few words altered:
The best two variates that we have chosen from a group of variates need not to contain either of the two best individual discriminators. It is essential to understand and accept the importance of this rule!
Of course, as we could see before, the conclusion doesn't seem to be so obvious, at least intuitively, and it somehow opposes the usual opinion. It is believed that the presence of strong stochastic relationship between two variates leads to redundancy regarding informativeness we get from each of them individually comparing to the case when we join them into the new feature vector, or use them as discriminators in the same discriminant function. Not only that we shouldn't neglect the one of the variates, but also we can observe that the situation of mutually highly correlated variates may lead to the case of STRONG SYNERGISM. Opinions were very diverse when this theory first appeared, more than a half of a century ago. It simply didn't look like possible to have strongly, statistically correlated features that could produce anything more but rather low-informative system.