![\begin{displaymath}
J=\int[p(X\vert C_1)-p(X\vert C_2)]log\frac{p(X\vert C_1)}{p(X\vert C_2)}dX
\end{displaymath}](img1.png) |
(1) |
One of the most useful criteria used in feature selection problems (you can learn more about information measures here ) is Divergence, J, defined as:
![\begin{displaymath}
J=\int[p(X\vert C_1)-p(X\vert C_2)]log\frac{p(X\vert C_1)}{p(X\vert C_2)}dX
\end{displaymath}](img1.png) |
(1) |
where p(X|Ci), i=1,2 are conditional probabilities of feature vector X, with respect to the given class i. X is d-dimensional feature vector. This measure of distance between two classes is especially convenient for the case of Multivariate Normal Gaussian Distribution of feature vector over class domains of classes C1 and C2.
If Mi and Si, i=1,2 represent mean vector and covariance matrix in each of the class i, then divergence could be written in suitable form:
| (2) |
where T denotes matrix transpose, and 'tr' denotes trace, which in case of equal covariance matrices, yields the Mahalanobis distance , M ,:
| (3) |
Now, consider a 2-class, 2-feature problem. I am going to derive the relation that connects joint divergence J(x1,x2) of two features x1 and x2 with their individual divergences:
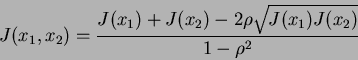 |
(4) |
where ![]() is the correlation coefficient between x1 and x2.
is the correlation coefficient between x1 and x2.
The following are definitions for the feature vector, X, the mean vectors, and the covariance matrices:
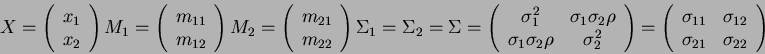 |
(5) |
You have probably noticed that covariance between two features (
![]() )
was expressed in terms of the correlation coefficient(
)
was expressed in terms of the correlation coefficient(![]() ). Also, notice that x1 and x2 could be replaced by any pair of individual features xi and xj from feature vector X.
). Also, notice that x1 and x2 could be replaced by any pair of individual features xi and xj from feature vector X.
Inverse of correlation matrix is given by:
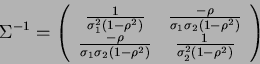 |
(6) |
The individual divergences (describing the distance between two classes separated in one feature space) are given in the following:
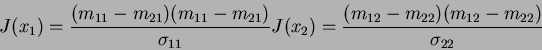 |
(7) |
Regarding the above results, we can write:
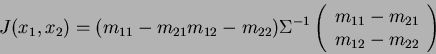 |
(8) |
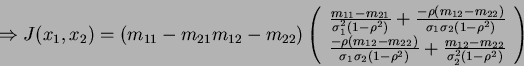 |
(9) |
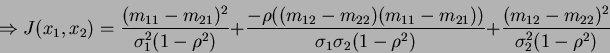 |
(10) |
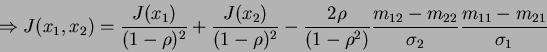 |
(11) |
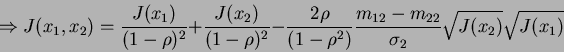 |
(12) |
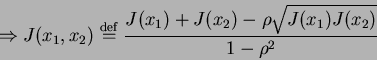 |
(13) |