Ranges of Redundancy and Synergism with respect to Correlation Coefficient

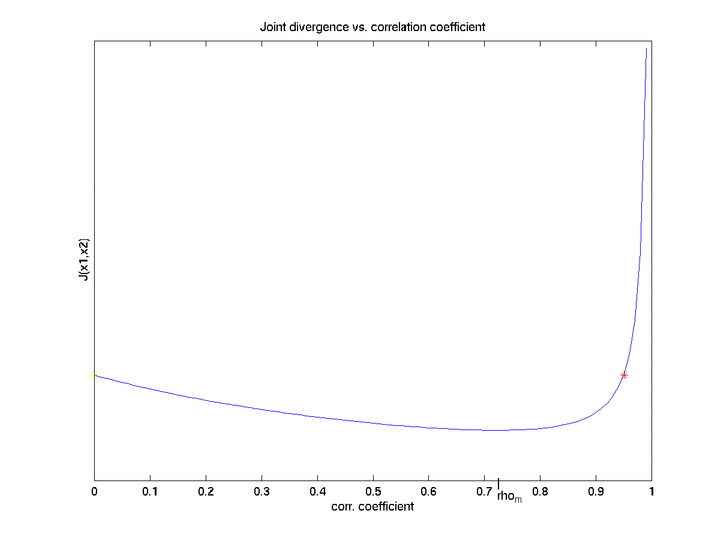
Assume that the class means are positively correlated and J(x₁)>J(x₂). The goal here is to find the range of correlation coefficient between two features inside which they are redundant, and then make some conclusions about joint features' behavior outside that range.

Definition: Features are redundant if their joint divergence is less than or equal to the sum of their individual divergences.

Take a look at the function of Divergence vs. Correlation Coefficient:

Since the above derived equation of the joint divergence is the quadratic equation we can test the nature of its roots. We have two solutions for rho that give us the value of J(x₁)+J(x₂) for the joint divergence J(x₁,x₂). From the following equation:

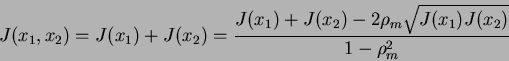$$J(x_1,x_2)=J(x_1)+J(x_2)=\frac{J(x_1)+J(x_2)-2\rho_m\sqrt{J(x_1)J(x_2)}}{1-\rho_m^2}$$ (14)

we have the following solutions for $\rho_m$: one is at the point $\rho_m=0$, and the other one is at $\rho_m=\frac{2\sqrt{J(x_1)J(x_2)}}{J(x_1)+J(x_2)}$.
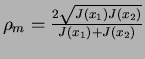Thus, for correlation ceofficients that are equal to zero and some other value (rho_m) we have borders of redundancy interval, at which divergence reaches the value equal to the sum of joint divergences (borders are depicted with yellow and red stars for correlation of zero and rho_m, respectively). 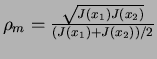And,with more careful observation of the latter result, we can see that the other solution $\rho_m$ could be expressed as $\rho_m=\frac{\sqrt{J(x_1)J(x_2)}}{(J(x_1)+J(x_2))/2}$ which is actually amazing since we have the ratio of geometric and arithmetic means of individual divergences. As my Prof. Godfried T. said- it really looks like someone fixed the result.

It is only left to be proved that the features are redundant inside the $[0,\frac{2\sqrt{J(x_1)J(x_2)}}{J(x_1)+J(x_2)}]$ interval. We have closed interval $[0,\frac{2\sqrt{J(x_1)J(x_2)}}{J(x_1)+J(x_2)}]$ in which the function (the divergence) is continuous, and at which ends the function has the same values. Hence, it is sufficient to show that the first derivative of the function is negative at the point $\rho=0$, and prove that this is really the interval of feature redundancy. From the definition of joint divergence, we can calculate the first derivative, and evaluate it to $-2\sqrt{J(x_1)J(x_2)}$ at $\rho=0$, which is obviously negative.

The maximum level of redundancy is at minimum of the divergence function (which is logical, since for the minimum divergence we have the minimum possible class separation, or better say, maximum overlapping, and hence, the greater piece of the information we are able to extract is common for both of the classes, which gives rise to lower discriminating power between classes. This level of redundancy (maximum) is found through setting the first derivative of the divergence function to zero, and solving the equation with respect to $\rho$.

If we set (for the sake of simplicity) A=J(x₁)+J(x₂), and $B=\sqrt{J(x_1)J(x_2)}$, then we have:

$$\frac{dJ(x_1,x_2)}{d\rho}=\frac{d}{d\rho}[\frac{1}{1-\rho^2}](A-2B\rho)+\frac{(-2B)}{1-\rho^2}$$ (15)

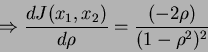$$\Rightarrow \frac{dJ(x_1,x_2)}{d\rho}=\frac{(-2\rho)}{(1-\rho^2)^2}$$ (16)

When zero, the above expression becomes:

$$2\rho(A-2B\rho)-2B(1-\rho^2)=0$$ (17)

which yields (after some trivial transformations):

$$\rho^2-\frac{A}{B}\rho+1=0$$ (18)

From the above we have two solutions for $\rho$:

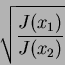$$\sqrt{\frac{J(x_1)}{J(x_2)}}$$ (19)

or

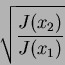$$\sqrt{\frac{J(x_2)}{J(x_1)}}$$ (20)

If you can recall , we made the assumption that J(x₁)>J(x₂) without any loss of generality (we could do the other way around letting J be greater for feature x₂), and, hence, only one solution is valid, so that we can conclude that the maximum level of redundancy is reached for:

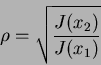$$\rho= \sqrt{\frac{J(x_2)}{J(x_1)}}$$ (21)

And, what is interesting to notice here is that we have the following:

The joint divergence at the maximum level of redundancy is equal to the greater of individual divergences of two features

J(x₁,x₂)=J(x₁) (22)

With the initial assumption that classes (the class means, actually, since we are talking about the Gaussian Multivariate Distribution) are positively correlated, the range of features' synergism is given for values of correlation coefficient greater than: 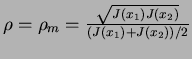$\rho=\rho_m=\frac{\sqrt{J(x_1)J(x_2)}}{(J(x_1)+J(x_2))/2}$, and for $\rho\to\infty$ we have the error free recognition, and $J(x_1,x_2)\to\infty$. For the positive correlation between the classes (the class means), every negative correlation coefficient between features will give rise to their synergism, and divergence will tend towards infinity for $\rho\to-1$.

For negative correlation between the class means, the situation is similar, just this time the redundancy interval is given on the negative part of the $\rho$ axis (the function is reflected image of the Divergence for positively correlated means-with respect to the J-axis) and every positive correlation between individual features will lead towards synergism of joint features.

<< >>