This technique uses the fact that a rigid displacement of an object (excluding reflections) can be fully specified by the knowledge of the displacements of three of its points that are non collinear (point_match).
Although in a noiseless situation three points is the absolute minimum, more points must be used in practice to ensure that the match is more robust (i.e., less sensitive to uncertainty in the positions of the points). The match is then defined in the least-square sense.
An efficient and stable algorithm for homologous point matching
registration uses singular value decomposition (SVD)
[2,54,55]. This algorithm may be described
by considering two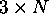 
matrices 
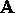and 
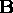whose
columns are the coordinates of points in two spaces related by a
rotation. The goal of the registration procedure is to find the
rotation matrix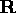 
such that 
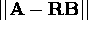is minimum. It can be shown that the least square rotation matrix is
where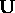 
and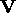 
are the matrices obtained from the singular
value decomposition of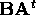 
:
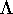is the diagonal matrix whose elements are the
singular values, an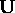d 
and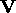 
are 
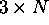and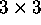 
unitary matrices respectively. However, some precautions
must be taken when the points are nearly coplanar, since in these
cases, the above algorithm can lead to a reflection transformation
instead of a rotation. In such situations, the least square rotation
matrix is simply obtained by changing the sign of the column of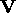 
that corresponds to the singular value that is close to zero (if
there is no such singular value, which is very unlikely, the algorithm
fails).
Neelin et al. [42] present an extensive analysis of
homologous point registration error, using both real and simulated
data. One most important conclusion of this study is that for N
homologous pairs the registration error goes down as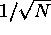 
for
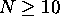when the measurement noise is Gaussian and of zero mean.