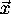 and
and 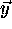 represent the same vector expressed in two different coordinate
systems, and related by the following expression:
represent the same vector expressed in two different coordinate
systems, and related by the following expression:
The registration procedure allows the determination of the linear
relationship between two coordinate systems. Let 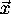 and
and 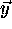 represent the same vector expressed in two different coordinate
systems, and related by the following expression:
represent the same vector expressed in two different coordinate
systems, and related by the following expression:
where 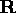 is a rotation matrix,
is a rotation matrix, 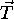 is a vector
giving the translation between the coordinate systems and s is a
scale factor. Together,
is a vector
giving the translation between the coordinate systems and s is a
scale factor. Together, 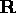 and
and 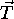 unambiguously describe
any arbitrary rigid body transformation. In a real registration,
measurement errors will prevent one from finding the exact
transformation. In fact the derived transformed coordinate system will
in general be slightly rotated, translated and scaled with respect to
the exact one. This can be expressed by:
unambiguously describe
any arbitrary rigid body transformation. In a real registration,
measurement errors will prevent one from finding the exact
transformation. In fact the derived transformed coordinate system will
in general be slightly rotated, translated and scaled with respect to
the exact one. This can be expressed by:
where 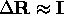 is a rotation matrix,
is a rotation matrix, 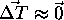 is a translation vector and
is a translation vector and 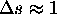 is the scaling error. approximate, written as
is the scaling error. approximate, written as
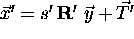 with
with 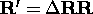 ,
, 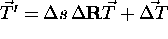 and
and 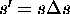 , clearly demonstrates the
fact that one can be mislead by merely comparing the rotation matrices
and the translation vectors to evaluate the registration error. Since
, clearly demonstrates the
fact that one can be mislead by merely comparing the rotation matrices
and the translation vectors to evaluate the registration error. Since
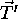 depends on
depends on 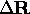 , a small rotational error can
make
, a small rotational error can
make 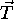 and
and 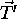 significantly different if the modulus of
significantly different if the modulus of
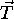 is large (which is often the case in ).
is large (which is often the case in ).
We define instead the registration error 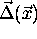 as follows:
as follows:
From exact and approximate: