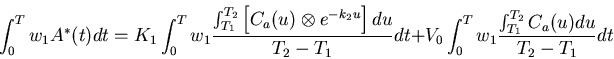Triple-Weighted Integration Method

In order to model the complete two-compartment system, we must be able to solve equation (4). In section 2.2, we solved the equation by multiplying by two different weights and then dividing, and we can take a similar approach with the full two-compartment equation. We can weight equation (4) with three different weights and then integrate:

$$\int_{0}^{T} w_{1}A^{*}(t)dt = K_{1} \int_{0}^{T} w_{1} \frac... ...{0}^{T}w_{1} \frac{\int_{T_1}^{T_2} C_{a}(u) du}{T_2 - T_1} dt$$ (7)

$$\int_{0}^{T} w_{2}A^{*}(t)dt = K_{1} \int_{0}^{T} w_{2} \frac... ...{0}^{T}w_{2} \frac{\int_{T_1}^{T_2} C_{a}(u) du}{T_2 - T_1} dt$$ (8)

$$\int_{0}^{T} w_{3}A^{*}(t)dt = K_{1} \int_{0}^{T} w_{3} \frac... ...{0}^{T}w_{3} \frac{\int_{T_1}^{T_2} C_{a}(u) du}{T_2 - T_1} dt$$ (9)

By multiplying equation (7) by $V_{0} \int_{0}^{T} w_{3} {(\int_{T_1}^{T_2}C_{a}(u)du)}/{(T_2 - T_1)} dt$and equation (9) by $V_{0} \int_{0}^{T} w_{1} {(\int_{T_1}^{T_2}C_{a}(u)du)}/{(T_2 - T_1)} dt$, and then subtracting the two, we may eliminate the V₀ term. A similar operation can be performed on equation (8) and equation (9). This leaves two equations that do not contain V₀. They may then be divided to produce:

$$\hspace*{-1.0cm} \frac{ \begin{array}{lcr} \multicolumn{2}{l}... ...(T_2 - T_1)}\, dt} \end{array} \end{array} \!\!\!\! \right\} }$$ (10)

The K₁ term cancels out of both the numerator and denominator of equation (10), leaving an equation that only involves k₂. As with the equation in section 2.2, this is very difficult to solve for k₂. Therefore, a look-up table was again used. Once the table matching values of k₂ with values of the right hand side of equation (10) has been created, we may evaluate k₂ through simple lookup. With the k₂ data computed, finding K₁ is simply a matter of evaluating either the numerator or denominator of equation (10) without cancelling K₁. With both K₁ and k₂ known, we may find V₀ by evaluating equation (4).