



Next: Rendering
Up: Measurement in scanner
Previous: MR Geometrical Distortions
The determination of the image space position corresponding to given
physical space location is what is all about. This can be
achieved, once the transformation 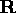 has been estimated (in
other words, once
has been estimated (in
other words, once 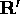 has been found), by using the inverse
transformation
has been found), by using the inverse
transformation 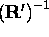 . But, in general, an arbitrary point
in physical space will map into a point for which the intensity in
image space have not been measured (recall that measurement in image
space is discrete). Moreover, the surgeon may want to look at the
image data through slices in arbitrary orientations (which is in
general different from the planes originally acquired). Then, the
interpolation of the image data is required, which is performed by
reformatting.
. But, in general, an arbitrary point
in physical space will map into a point for which the intensity in
image space have not been measured (recall that measurement in image
space is discrete). Moreover, the surgeon may want to look at the
image data through slices in arbitrary orientations (which is in
general different from the planes originally acquired). Then, the
interpolation of the image data is required, which is performed by
reformatting.
Reformatting can be defined in this particular case as the
mapping of image intensities of the model space (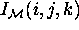 ) onto the points of an arbitrary plane taken through the model
space [40].
) onto the points of an arbitrary plane taken through the model
space [40].
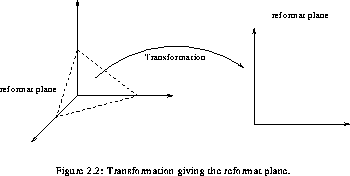
The orientation of the reformatted plane is fully determined if the
spatial coordinate of three of its points are known. If 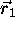 ,
,
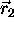 ,
, 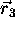 are the 3-D position vectors of these points in
scanner space and
are the 3-D position vectors of these points in
scanner space and 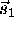 ,
, 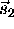 ,
, 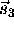 , their 2-D
positions in the reformatted plane, vectors in scanner space and in
the reformatted plane are related by the following relations:
, their 2-D
positions in the reformatted plane, vectors in scanner space and in
the reformatted plane are related by the following relations:
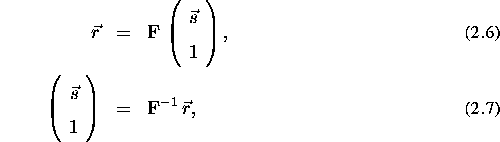
where
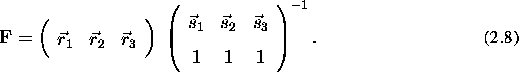
Note that 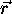 and
and 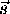 are
are  and
and 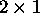 column vectors respectively. Once the transformation
column vectors respectively. Once the transformation 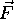 has
been defined, the values of intensity in the reformat plane can be
retrieved from the values in the scanner space.
has
been defined, the values of intensity in the reformat plane can be
retrieved from the values in the scanner space.

where 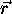 is given by s2r. The fact that the
intensity is not known at every arbitrary point implies that the value
at
is given by s2r. The fact that the
intensity is not known at every arbitrary point implies that the value
at 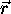 must be interpolated from the known values in scanner
space.
must be interpolated from the known values in scanner
space.
Patrice MUNGER
Mon Oct 23 15:09:17 EDT 1995
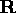 has been estimated (in
other words, once
has been estimated (in
other words, once 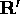 has been found), by using the inverse
transformation
has been found), by using the inverse
transformation 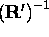 . But, in general, an arbitrary point
in physical space will map into a point for which the intensity in
image space have not been measured (recall that measurement in image
space is discrete). Moreover, the surgeon may want to look at the
image data through slices in arbitrary orientations (which is in
general different from the planes originally acquired). Then, the
interpolation of the image data is required, which is performed by
reformatting.
. But, in general, an arbitrary point
in physical space will map into a point for which the intensity in
image space have not been measured (recall that measurement in image
space is discrete). Moreover, the surgeon may want to look at the
image data through slices in arbitrary orientations (which is in
general different from the planes originally acquired). Then, the
interpolation of the image data is required, which is performed by
reformatting.
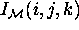 ) onto the points of an arbitrary plane taken through the model
space [
) onto the points of an arbitrary plane taken through the model
space [
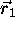 ,
,
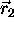 ,
, 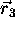 are the 3-D position vectors of these points in
scanner space and
are the 3-D position vectors of these points in
scanner space and 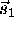 ,
, 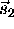 ,
, 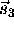 , their 2-D
positions in the reformatted plane, vectors in scanner space and in
the reformatted plane are related by the following relations:
, their 2-D
positions in the reformatted plane, vectors in scanner space and in
the reformatted plane are related by the following relations:
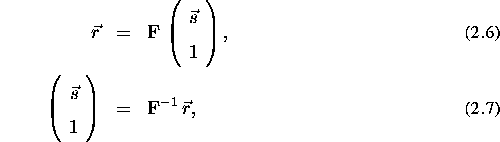
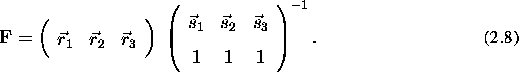
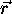 and
and 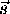 are
are 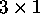 and
and 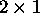 column vectors respectively. Once the transformation
column vectors respectively. Once the transformation 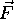 has
been defined, the values of intensity in the reformat plane can be
retrieved from the values in the scanner space.
has
been defined, the values of intensity in the reformat plane can be
retrieved from the values in the scanner space.

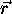 is given by s2r. The fact that the
intensity is not known at every arbitrary point implies that the value
at
is given by s2r. The fact that the
intensity is not known at every arbitrary point implies that the value
at 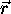 must be interpolated from the known values in scanner
space.
must be interpolated from the known values in scanner
space.