
Geometrical distortion of MR images is rather significant in the context of . This section describes this phenomenon, along with some correction methods.
In MR imaging, linear field gradients allow each point in space to be related to a resonance frequency. In one dimension, say x, this can be expressed by:

where 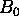 is the main magnetic field intensity,
is the main magnetic field intensity, 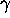 the
gyromagnetic ratio of the imaged spin and
the
gyromagnetic ratio of the imaged spin and 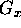 the magnetic field
gradient in the x direction. Since any conventional image
reconstruction algorithm relies on this relationship, non-uniformity
of
the magnetic field
gradient in the x direction. Since any conventional image
reconstruction algorithm relies on this relationship, non-uniformity
of 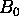 , non-linearity of
, non-linearity of 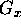 or susceptibility effects will
introduce errors on the spatial localization of the different
resonance frequencies.
or susceptibility effects will
introduce errors on the spatial localization of the different
resonance frequencies.
It is possible to classify MR geometric distortion source in three main groups [41]:
Machine-dependent distortions factors, including main field inhomogeneity, gradient field non-linearity and eddy currents caused by the gradient switching, can in some cases be corrected for by careful calibration of the scanner and by phantom studies. It has been shown [6] that the contribution of gradient non-linearity to the distortion is stable and that it can be corrected for independently of the other distortion factors. Also, Michiels et al. [41] demonstrate that for 3-D spin-echo and gradient-echo sequences, the spatial misregistration introduced by main field inhomogeneity and gradient field non-linearity is:
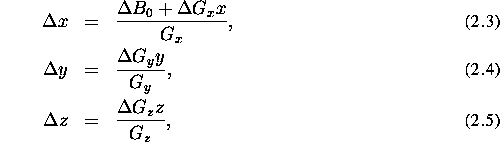
where 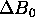 represents the main field inhomogeneity,
represents the main field inhomogeneity, 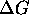 the gradient field non-linearity and x is the direction of the
read-out gradient. With the spin warp imaging method, each phase
encoding step is performed with a different gradient magnitude (but
the gradient is applied for the same time interval). So, the effect of
field inhomogeneity in the phase encoding direction is to introduce a
space-variant but time-invariant phase shift in that direction (since
this gradient is turned off during readout). Since only the magnitude
of the complex image is eventually displayed, this phase shift is of
no consequence for the final image. Sumanaweera et al.
[60] describe a method relying on this phenomenon to
quantify field inhomogeneity. The principle of this technique is to
acquire two images with the readout gradient in orthogonal directions.
Any imaged object can be considered to be accurately positioned in the
phase encoding direction. In this manner, the true position of the
object can be found by combining the information given by the two
images. Schad et al. [51] describes a geometric distortion
study using phantoms of known geometry. One phantom was used to
correct for in-plane distortion while another was used to correct for
the slice profile distortion. This distortion correction reduced the
error on the localization of a target using a stereotactic equipment
from 3 mm to 1 mm, where the reference was the localization of the
points using a CT scan. However, this method does not allow for
correction of distortions induced by patient susceptibility
variations. A comparison of the localization accuracy between CT and
MR based stereotaxy, made by Kondziolka at al. [34],
reports a localization difference around 2 mm between the two
modalities. The authors note that the observed difference can be
entirely attributed to observer variability in the selection of the
target.
the gradient field non-linearity and x is the direction of the
read-out gradient. With the spin warp imaging method, each phase
encoding step is performed with a different gradient magnitude (but
the gradient is applied for the same time interval). So, the effect of
field inhomogeneity in the phase encoding direction is to introduce a
space-variant but time-invariant phase shift in that direction (since
this gradient is turned off during readout). Since only the magnitude
of the complex image is eventually displayed, this phase shift is of
no consequence for the final image. Sumanaweera et al.
[60] describe a method relying on this phenomenon to
quantify field inhomogeneity. The principle of this technique is to
acquire two images with the readout gradient in orthogonal directions.
Any imaged object can be considered to be accurately positioned in the
phase encoding direction. In this manner, the true position of the
object can be found by combining the information given by the two
images. Schad et al. [51] describes a geometric distortion
study using phantoms of known geometry. One phantom was used to
correct for in-plane distortion while another was used to correct for
the slice profile distortion. This distortion correction reduced the
error on the localization of a target using a stereotactic equipment
from 3 mm to 1 mm, where the reference was the localization of the
points using a CT scan. However, this method does not allow for
correction of distortions induced by patient susceptibility
variations. A comparison of the localization accuracy between CT and
MR based stereotaxy, made by Kondziolka at al. [34],
reports a localization difference around 2 mm between the two
modalities. The authors note that the observed difference can be
entirely attributed to observer variability in the selection of the
target.
Patient-dependent factors, including susceptibility effects, chemical shift and flow, cannot be corrected ``once and for all'' since they depend on the particular anatomy of each patient. Distortion correction for objects of known shape and composition (fiducial markers for example) can be performed by means of an analysis of the susceptibility distortion induced by such objects. Sumanaweera [59] gives an example of this for a cylindrical fiducial marker. This technique requires the solution of the Laplace equation for the magnetic potential with boundary conditions, which implies that analytical solutions can only be obtained for highly symmetrical objects, and numerical methods must be employed for other cases. The application of this technique for highly variable shapes such as the human head, reported by Shizhe et al. [53], gives a good indication of the importance of local magnetic field distortion that can be induced by the patient.