Registration comparison in the clinical situation

The goal of this study was to determine the size of the registration error and the variability involved in registrations performed in the clinical environment (operating room) when procedures were performed using 3-D images based on MR data. Although these results have a limited statistical significance and bring few insights to the mechanism of registration, they demonstrate that the registration process using MR images is far from trivial, and that the accuracy currently available using the standard approach is 4 mm at best.

These measurements were performed using the following protocol.

1. During a depth electrode implantation procedure, in which the OBT stereotactic frame (see Chapter 1) is installed on the patient's head, two registrations were performed.
   • The first was performed by homologous point matching on the corners of the frame markers (4 points). This was accomplished by touching the intersection of the frame markers using the surgical probe and by selecting the corresponding point in the 3-D data set. Three orthogonal planes were used (sagittal, coronal and axial) to ensure an accurate localization of the corner. It must be mentioned that the markers of the frame, being surrounded by a thin layer of Plexiglas, were not directly accessible physically. However, the thickness of the Plexiglas layer was approximately corrected for by selecting points slightly beside the corner seen on the images. The error in the localization of the point in the associated image, however, is probably less than 1 mm.
   • The second registration was achieved by surface matching the computer model to the patient's head. The surface points (40) were randomly scattered on the surface. Prior to the surface matching, a rough homologous point match was performed in order to arrive at an approximate solution. This preliminary registration used four anatomical external landmarks, usually the two outer canti and one point on each ear, identified on the 3-D rendering of the skin surface.
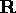2. The registration parameters were extracted from the registration log files that are compiled by the Viewing Wand program. These files contain the rotation matrix , the translation vector 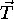and the scale factor S that constitute the transformation between the imaging and surgical spaces:

    

3. The difference between the two registrations was computed according to reg_error for points along the three axes of model space. The modulus of the difference was then plotted, as shown in first_patientlast_patient.

It is not immediately obvious why these graphs are curved lines, since they represent the distance between two straight lines in 3-D space. However, if the lines are represented as:

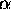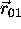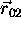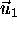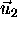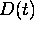where is a scale parameter, and are points belonging to the lines, and are unit vectors parallel to them and t is a parameter labelling points on them, we can compute the difference between corresponding position t on theses lines:

This will give a ``v-shaped'' function if:

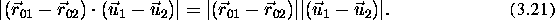
So, the graphs are straight if 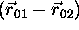is parallel to 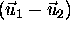or if one of these vectors is zero. In all other cases, the line will be curved.

It can be shown that the curve reaches a minimum value when:

where 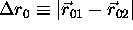, 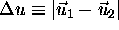and 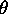is the angle between 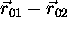and .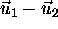

In order that the minimum be at the origin, let 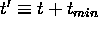. distance then becomes:

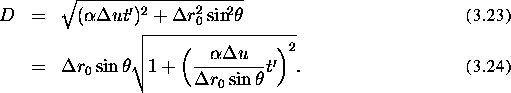
When 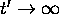, 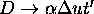i.e., the distance between the lines increases linearly. When 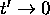, we can develop D in a Taylor series:

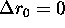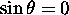This shows that the curvature becomes infinite, i.e., the graph is v-shaped, if or . If 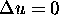, i.e., there is no rotational error and 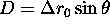is constant.

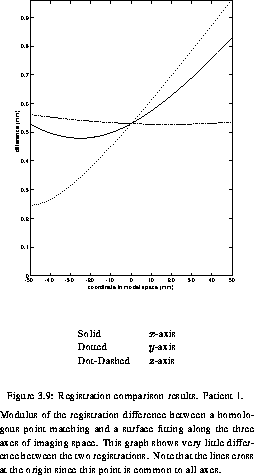
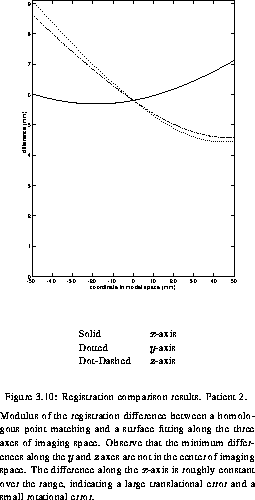
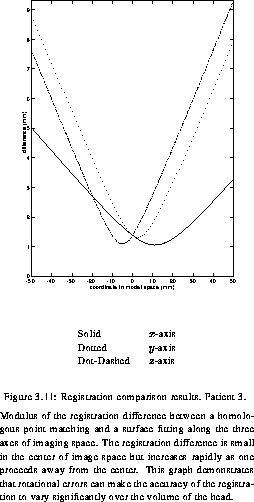
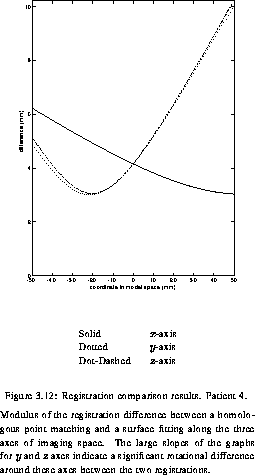
first_patient shows a sub millimetric difference between the two registrations over the volume of 1000 cubic mm. The situation is quite different for the three other patients, where large differences can be observed. The graph for Patient 2 (second_patient), reveals a difference at the origin of 6 mm. This means that, if the surgeon holds the probe at the point corresponding the the origin of the scanner space (roughly in the center of the head), the position of the probe displayed on the screen would differ by 6 mm for the two registrations. Moreover, we can see that the minimum difference is around -25 mm along the x-axis and around +40 mm along the two other axes. This illustrates the fact that even though the registration error is likely to be minimum at the origin, it is not always the case. third_patient shows an example where the rotational error makes the difference between the two registrations increase rapidly, demonstrating that the registration error can be dramatically space-variant. Since the experimental protocol was consistent across the four patients, we believe that the discrepancy observed between the first patient and the other three is due to statistical fluctuation.

As will be demonstrated in Chapter 5, the image of the corners of the frame markers can be subject to displacements from their real position by approximately 2 mm on average. This, coupled with the imprecision due to the fact that it is not possible to physically reach the intersection points of the markers, makes the uncertainty on the point position to be approximately 3 mm. The observation of simul_4_3 shows that the observed errors are certainly possible, although a rigorous comparison is not possible since the curve in simul_4_3 and the curves in figures first_patientlast_patient do not represent the same thing (the latter result represents differences between two different registration techniques while the first is the expected difference between different registrations performed with the same registration technique).