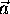 and
and 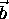 belonging to C1 and C2 respectively such
that the distance between them is the smallest possible. Let
the equations of C1 and C2 be:
belonging to C1 and C2 respectively such
that the distance between them is the smallest possible. Let
the equations of C1 and C2 be:
Once each channel has been fitted to a line, the intersection of any
two channels C1 and C2 can be computed by finding the two points
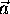 and
and 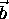 belonging to C1 and C2 respectively such
that the distance between them is the smallest possible. Let
the equations of C1 and C2 be:
belonging to C1 and C2 respectively such
that the distance between them is the smallest possible. Let
the equations of C1 and C2 be:

Since the shortest distance between a point and a line is that measured perpendicularly to the line, the shortest line segment between C1 and C2 is perpendicular to both of these lines. This can be expressed vectorially by:
where C is a constant. Furthermore, the fact that  and
and 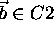 gives the equations:
gives the equations:

which can also be written:
The seven scalar unknowns that constitute 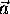 ,
, 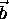 and C
can be determined by using the three scalar equations given by the
vectorial equation paral together with the four independent
scalar equations given by the vectorial equations in1 and
in2.
and C
can be determined by using the three scalar equations given by the
vectorial equation paral together with the four independent
scalar equations given by the vectorial equations in1 and
in2.