



Next: MATLAB Implementation
Up: Mathematical Analysis
Previous: Triple-Weighted Integration Method
Delay and Dispersion Correction
Since the blood samples used to estimate Ca(t) are taken from the
subject's arm, the activity data gathered from them must be corrected
for delay and dispersion within the body. In order to perform the
delay correction, we used the technique of Iida, by performing a
least squares fitting of the equation:
![\begin{displaymath}A^{*}(t) = \frac{\int\limits_{T_1}^{T_2} \left( \alpha \left[...
...
e^{-\beta t} \right] + \gamma C_a(t) \right) dt} {T_2 - T_1}
\end{displaymath}](img14.gif) |
(11) |
where A*(t) in this case is the average activity over grey
matter,
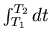 represents integration over frames,
represents integration over frames,
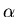 ,
,
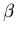 ,
and
,
and 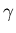 are the fitting parameters, and
Ca(t) is the blood data. The delay itself enters this equation by
generating Ca(t) from:
are the fitting parameters, and
Ca(t) is the blood data. The delay itself enters this equation by
generating Ca(t) from:
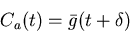 |
(12) |
The function 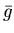 is the result of performing dispersion
correction on the blood sample data. This is represented by the
equation:
is the result of performing dispersion
correction on the blood sample data. This is represented by the
equation:
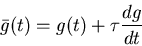 |
(13) |
which is an implicit deconvolution of the equation:
![\begin{displaymath}g(t) = \bar{g}(t) \otimes \left[ \frac{1}{\tau} e^{\frac{-t}{\tau}}
\right]
\end{displaymath}](img22.gif) |
(14) |




Next: MATLAB Implementation
Up: Mathematical Analysis
Previous: Triple-Weighted Integration Method
Mark Wolforth
<wolforth@bic.mni.mcgill.ca>
Greg Ward
<greg@bic.mni.mcgill.ca>
Sean Marrett
<sean@bic.mni.mcgill.ca>
![\begin{displaymath}A^{*}(t) = \frac{\int\limits_{T_1}^{T_2} \left( \alpha \left[...
...
e^{-\beta t} \right] + \gamma C_a(t) \right) dt} {T_2 - T_1}
\end{displaymath}](img14.gif)
![]() is the result of performing dispersion
correction on the blood sample data. This is represented by the
equation:
is the result of performing dispersion
correction on the blood sample data. This is represented by the
equation: