Consider the case with two linearly separable classes. The training data can be formalized as the following:

[formalization of training data]

This is illustrated using a dataset with N=2, l=20 and two classes (blue and green).

There are an infinite number of support vectors that can be used to separate the two classes. However, as described, the SVM chooses the linear separator with the maximum margin. This can be formalized as the following:

[inequality for margins.]

In addition, there is the added constraint that the maximum margin can be determined as the minimum summed distance between a hyperplane and the closest points from each class.

[equation for minimum w.]

This results in the following Lagrangian formalization, the value of which we want to maximize to determine the maximum margin:

[Lagrangian for linearly separable margin]

The maximum margin is indicated in red in the image below.

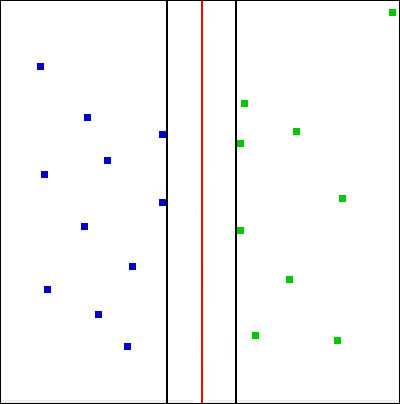
In the next section, we will see how the maximum margin can similarly be obtained from convex hulls.