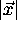
A simple comparison of two registrations is in many cases of little help for determining the characteristics of: 1) the expected registration error and 2) the variability from one registration to the other for a given registration method. This is because in any realistic situation, the true ``best'' transformation is not known a priori. In this section, we analyze the behavior of registration error characteristics averaged over a large number of trials. This provides, at least in principle, a means of characterizing registration methods.
Returning to the formulation introduced in section
3.1, it is interesting to compare not only two
registrations but a large number (N) of them. For this, we consider
the mean square ( MS) error as a function of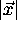 
:
Using reg_error and
applying the cosine law twice, we observe that:
where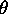 
is the angle between 
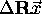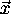and 
, and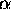 
is the angle between 
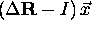and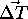 
. The derivation of
modulus uses the fact that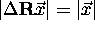 
(since 
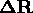is a rotation matrix).
Now, if N registrations are performed, the MS error will be:
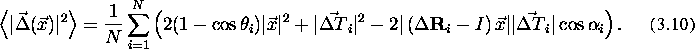
If N is sufficiently large the last term in the expression will
vanish since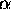 
can take any value between 0 and 
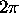. This
will make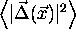 
independent of the direction
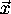. Furthermore, under the assumption that 
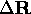is
close to the unit matrix,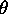 
will be small and 
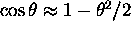. The MS registration error then becomes:
where r has been used instead of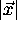 
and
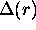instead of 
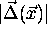. It is important to
note that for any individual registration, the angle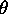 
by
itself is of little significance since it depends on the direction of
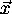. MS_reg_error shows that the MS registration
error increases with the modulus of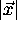 
and is related to the
individual MS of 
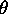and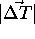 
.
It is also instructive to look at the variability of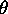 
and
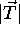between registrations. This can be performed by computing
the variance of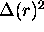 
defined by:
Evaluating the squared term in the summation var_def shows that:
The first term is:
Using var_dev and MS_reg_error, we find:
This equation allows us to estimate the variability of the registration from the standard deviation of the registration error along a radial line. It shows, as in the case of the mean squared error, that the variance of the squared registration error increases with the distance from the origin.
