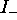 ) with
) with 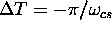 . The three acquisitions can be written:
. The three acquisitions can be written:
The three-point Dixon technique [22] extends
the above method by adding a third acquisition (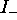 ) with
) with 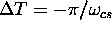 . The three acquisitions can be written:
. The three acquisitions can be written:
where the M's and the 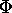 's represent the modulus and the phase
of the acquired images and
's represent the modulus and the phase
of the acquired images and 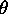 is a phase shift common to all
three acquisitions. This phase factor is easy to remove since it is
equal to
is a phase shift common to all
three acquisitions. This phase factor is easy to remove since it is
equal to 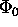 . Let
. Let
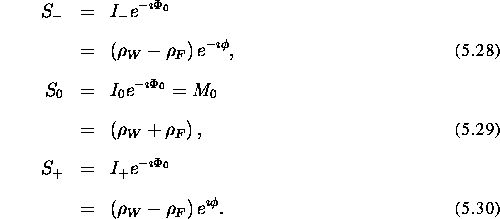
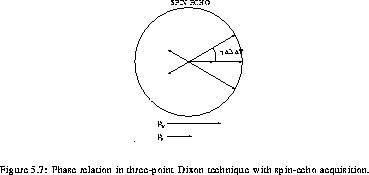
The third acquisition makes it possible to determine 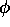 since:
since:
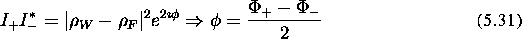
Since the argument of  is only unambiguous between
is only unambiguous between 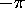 and
and 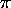 ,
, 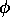 can be determined directly from the last equation
only if it is between
can be determined directly from the last equation
only if it is between 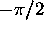 and
and 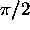 . This would require the
size of the field inhomogeneity to be smaller than
. This would require the
size of the field inhomogeneity to be smaller than
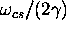 which is certainly not acceptable. However,
under the assumption that the gradient of the inhomogeneity-induced
phase shift is limited to a certain value, it is possible to
unwrap the phase, i.e., to find the phase from its
principal value between
which is certainly not acceptable. However,
under the assumption that the gradient of the inhomogeneity-induced
phase shift is limited to a certain value, it is possible to
unwrap the phase, i.e., to find the phase from its
principal value between 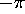 and
and 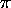 . A method for unwrapping the
phase is presented by Glover and Schneider [22]. Song et
al. [57] also present a technique to unwrap the phase by
solving the Poisson equation with appropriate boundary conditions.
. A method for unwrapping the
phase is presented by Glover and Schneider [22]. Song et
al. [57] also present a technique to unwrap the phase by
solving the Poisson equation with appropriate boundary conditions.
Once 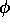 is known, by unwrapping
is known, by unwrapping 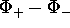 and dividing by
two, the water and fat images can easily be obtained. Letting
and dividing by
two, the water and fat images can easily be obtained. Letting
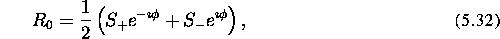
we find: