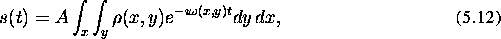
Another issue that is of interest in is patient-induced susceptibility distortion, which can be important wherever a sharp variation in the magnetic susceptibility is present. Although magnetic susceptibility variations may not be significant deep inside the brain, they can constitute a real problem near the surface of the skin or near bone-air interfaces at the skull-base. Since many registration techniques rely on the use of surface structures, it is important to assess potential errors of this nature.
The goal of this section is to investigate the possibility of using the three-point Dixon imaging technique [22,21] to acquire magnetic field maps of a human subject. The field map gives a direct representation of the static field inhomogeneity, allowing the measurement of the spatial misregistration associated with each point of an image. Typically, such a field map can be obtained by computing the phase difference between two images acquired with different echo times.
In order to understand how this works, consider a general 2-D Fourier image acquisition. The received signal, after low pass filtering can be written:
where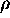 
is the weighted spin density, and A, a proportionality
constant. This equation expresses the fact that the signal can be
considered as a superposition of harmonic oscillators whose
frequencies and amplitudes are space-variant.
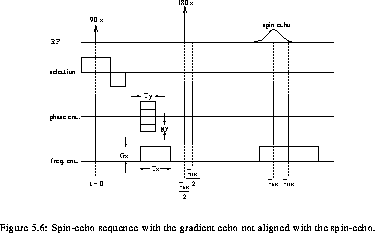
For a typical spin echo sequence (se_seq), the phase
distribution, including the effect of main field inhomogeneity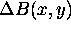 
, can be written:
where
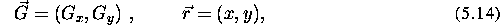
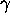is the gyromagnetic ratio 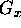and 
and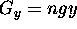 
the
magnetic field gradient in the x and y directions respectively.
gy represents the increment unit of the phase encoding gradient
amplitude. The first term in gen_phase represents the phase
distribution immediately after the application of th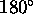e 
pulse
.
The evaluation of gen_phase for the sequence of se_seq gives:
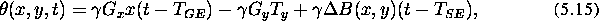
By letting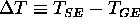 
,
this becomes:
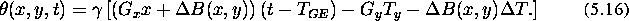
Replacing the last equation in gen_sig we obtain for the
signal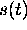 
:
where
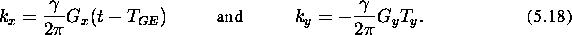
It can be seen from the sig that the reconstructed image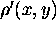 
(by inverse Fourier transform) will be:
So, if the gradient echo and the spin echo coincide (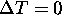
),
which is normally the case,
the reconstructed image is real. Otherwise, the reconstructed image
contains a phase factor that depends on the field inhomogeneity
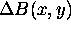. In theory, as shown by rec_im,
only one image would be necessary to reconstruct the field map.
However in practice, other sources of dephasing are present and it
is desirable to subtract the phases of two images acquired with
different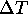 
in order to keep only contributions to the
dephasing that are due to field inhomogeneities.
Another problem is encountered in reality. Since the precession
frequency of protons in fat is slightly lower than that of protons in
water, fat protons can be interpreted as water protons in a different
(lower) magnetic field. If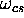 
is the difference between the
precession rate of protons in fat and in water, the corresponding
field offset is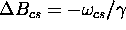 
. This can be
expressed mathematically by writing the reconstructed image as the sum
of contributions from fat and water:
If one were to acquire a field map, the extra phase factor associated with the fat signal would be impossible to distinguish from that associated with field inhomogeneities.
The two-point Dixon technique [14] allows the
water and fat signals to be separated. The principle of this technique
is to acquire two images, one (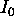
) with 
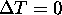, and the
other (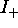
) with 
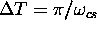(this implies that
the reversing pulse must be applied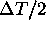 
earlier as that in a
normal spin-echo acquisition). From wf_sig the equation of
the two images is:
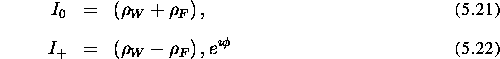
where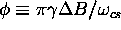 
.
In the absence of field inhomogeneity (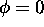
), the fat and water
images are given by:
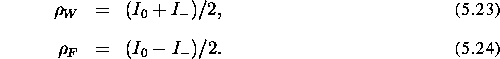
Otherwise, the presence of inhomogeneities makes the exact separation
of water and fat images impossible. Note that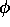 
cannot be
obtained from 
since the sign of 
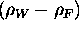is not
known.
