This allowed us to investigate what the pointed region of the coil would do to the magnetic field.  Figures 15, 16 and 17 illustrate the theoretical distribution for one lobe.  The results indicate that the distribution is very similar to a simple circular coil except that for close distances from the coil there is a prominent peak at the points where there is a bend in the coil.  The peak seems to diminish as the distance above the point becomes greater.

   As you move further away from the coil, the peak seems to become rounded and less prominent.  The magnitude of the peak field also becomes small as you move further away from the coil.

   An image of the output voltage carrying with time was seen on an oscilloscope (detected with a single loop pick up coil).  The signal was a cosine with a peak to peak voltage of 50 +/- 1mV and a period of 200+/- 2s.

    The SMP was used to collect the data for all three components of the magnetic field simultaneously.  The data for the three components were saved in independent files and the proper conversion into voltage was done by converting the DAC output into voltages according to the calibration curve for the DAC.  Once the voltage is known, the magnitude of the magnetic field was calculated for each data point by noting that the voltage measured is the integrated voltage over the effective surface area.  The conversion factor in terms of the integrating circuit ws determined to be 6 X 10^-3+/- 2 X 10^-3 .  This factor comes from the analysis of the integrator as shown in the Set Up section.  We know that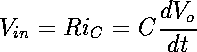

                                        (15)

and

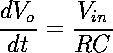                                                        (16)

where R is the resistor in the integrator, C is the capacitor and i is the current.  Vin is the input voltage and Vo is the output voltage.

    Therefore, .  We also know that where S is the effective surface area.

    Combining all of these together we get a conversion factor in the form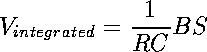

                                                        (17)

where B is the magnetic field.  The voltage reading from the DAC was converted to voltage with the conversion factor of 1/204.8.

    The error on the magnetic field reading was determined by the conventional error analysis techniques.  That is, the resistor was assumed to have an error of 10% and the capacitor to have an error of 50% which is often the case.  Therefore, the equation for the error was determined to be: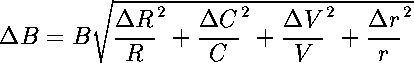

    (18)

where r is the radius of the effective area, V is the voltage reading from the DAC, C is the capacitor and R is the resistance.

    Figure 21 depicts the x components of the magnetic field at a distance of 1.1 +/- 0.5cm as determined experimentally from the SMP.

    The distance is defined with respect to the coil center, - i.e. center of the junction of the two tear shaped elements of the figure-eight coil.  The power on the Cadwell Stimulator was set at 50% of the maximal power output because the coil had overheating problems.  The current in the theoretical calculations for the program was determined by taking the total current at maximal power output and multiplying by , since power is proportional to the square of the current.

    The x component of the field was determined by orientation A of the SMP and the y component by orientation B of the SMP.  Finally, the z component of the magnetic field was determined by orientation C of the SMP.  Figures 21, 22, and 23 illustrates the results of each of the components of the magnetic field measured.  The square root of the squared sums of the three components would give us the 3-dimensional magnitudes of the magnetic field for some distance above the coil.  Figure 24 gives the experimental magnetic field distribution for a distance of 1.1 +/- 0.5cm above the TMS coil.  Figure 25 illustrates the theoretical distribution expected.

    The distribution was determined to have the shape that was expected from the theoretical calculations.  The prominent peak was found to have a magnitude of 0.4 +/- 0.24 Tesla at this distance experimentally.  There seems to be a discrepancy between the theoretical and the experimental results in terms of the magnitude.

    At a distance of 1.6 +/- 0.5cm, the distribution became more rounded in nature and the peak field diminished to 0.3 +/- 0.18T.  The theoretical peak intensity was found to be 0.45 T for this distance.  Figure 26 illustrates the resulting magnetic field distribution for 1.6 +/- 0.5cm above the coil and the corresponding theoretical distribution is shown in Figure 27.

    From the results, it seems that as the distance between the TMS coil and the SMP increased, a better correlation between the theoretical predictions and the experimental measurement could be made.  This is probably due to the measuring technique used in this experiment.  The SMP has a diameter of 1.0 +/- 0.1cm which is not significantly smaller than the diameter of the TMS coil itself.  The field produced by the TMS coil may not be fully characterizable by the SMP used here.

    The contribution of the z component measurement plays an additional part in the discrepancy of the shape of the magnetic field distribution.  In the orientation of the z component SMP, the distance from the TMS coil is the same at all points of measurement.  Figure 30 illustrates this effect.

    Since the field strength varies as 1/r², this would have a significant effect on the measurement.  That is, when the x and y components are being measured, the measurements would span for distances +/-0.5cm from the center of the SMP.  However, for the z component, the measurements only span for one distance.  The measurements for the x and y components were taken consistently with the same technique but the z component was determined by a slightly different method.  This may be the reason why the measured z component of the magnetic field is bigger that it should be.  If the contribution of the z component is decreased hypothetically, the distribution resembles the expected distribution more precisely.  Figure 31 illustrates this effect.

    The error produced due to the measuring technique for the z component could be corrected by making the SMP smaller in diameter.  The smaller the diameter of the SMP, the smaller the variation in the distance within the SMP form the TMS coil for the x and y component measurements and therefore, a more equalized measurement for all three components.

    However, the discrepancy in the magnitude of the magnetic field would lie in the uncertainty of the actual current being supplied into the TMS coil.  The current from the Cadwell unit was not measured at the 50% setting.  Rather, the manufacturer was contacted for the specifications.  To investigate the effect of the current on the magnitudes of the distribution, the current was decreased in our simulation to 1.5kA and re-constructed.  This is illustrated in Figure 32.

    The resulting simulation shown in Figure 31 seems to be closer to the experimental magnitudes previously found.  The error produced here can be rectified by taking a closer look at the power supply.  A calibration of the magnitude of the current form the current supply into the TMS coil as a function of the percentage indicated on the dial can be determined experimentally.  Once this is know, a better simulation of the actual magnetic field expected can be completed.

    There were also some uncertainties related to the exact configuration of the coil itself.  The TMS coil was mounted in a wooden box therefore the actual distance away from the coil you were measuring at was uncertain.  The xy translational device also contributed to the error since the motor slipped on occasion.