- 1.
- The function declaration line. The output arguments K1,
k2, and V0 will all be whole images--that is, for
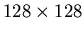 PET data, they will be matrices with 16,384
elements per column, and one column per slice processed.
delta will contain the blood delay term
PET data, they will be matrices with 16,384
elements per column, and one column per slice processed.
delta will contain the blood delay term 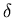 for each
specified slice.
for each
specified slice.
Of the input arguments, only filename (the name of the MINC
volume to process) and slices (the list of slices to process)
are required. The other three are boolean variables (i.e., they
should be scalars with a value of either 0 or 1) that default to
``true'' (1). progress controls whether RCBF2 prints
progress information; correction decides whether or not it
performs correction of the blood data for delay and dispersion; and
batch controls whether selection of the mask used for
delay/dispersion correction should be interactive or automatic (the
default). The latter two should not be changed when RCBF2 is
being used for real data analysis, and are merely provided to speed
things up when debugging.
function [K1,k2,V0,delta] = rcbf2_slice ...
(filename, slices, progress, correction, batch)
- 2.
- Initialize the matrices that will hold the K1, k2, and
V0 images, as well as the vector to hold the value of
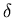 (the blood delay from equation 12) for each slice.
(the blood delay from equation 12) for each slice.
total_slices = length(slices);
K1 = zeros(16384,total_slices);
k2 = zeros(16384,total_slices);
V0 = zeros(16384,total_slices);
delta = zeros(1,total_slices);
- 3.
- Open the volume and get some preliminary information on frame
times and lengths.
img = openimage(filename);
if (getimageinfo (img, 'time') == 0)
error ('Study is non-dynamic');
end
FrameTimes = getimageinfo (img, 'FrameTimes');
FrameLengths = getimageinfo (img, 'FrameLengths');
MidFTimes = FrameTimes + (FrameLengths / 2);
- 4.
- Read the blood data, perform cross-calibration, and convert
units. (See explanation in section 3.3.1.)
[g_even, ts_even] = resampleblood (img, 'even');
XCAL = 0.11;
rescale(g_even, (XCAL*37/1.05));
- 5.
- Create the weighting functions, w1, w2, and w3 from
equations 7-9. Also here we
initialize the list of k2 values from which the lookup table will
be generated.
w1 = ones(length(MidFTimes), 1);
w2 = MidFTimes;
w3 = sqrt (MidFTimes);
k2_lookup = (-10:0.05:10) / 60;
- 6.
- At this point, we start the processing that is specific to each
slice: read the PET data, perform delay/dispersion correction,
generate the lookup table, and solve equation 10. Thus,
we loop through all user-specified slices:
for current_slice = 1:total_slices
- 7.
- Read in the PET data for the current slice, and rescale it
to convert from
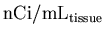 to
to
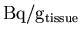 .
.
PET = getimages (img, slices(current_slice), 1:length(FrameTimes), PET);
rescale (PET, (37/1.05));
- 8.
- Compute the weighted integrals of the PET data.
PET_int1 = ntrapz (MidFTimes, PET, w1);
PET_int2 = ntrapz (MidFTimes, PET, w2);
PET_int3 = ntrapz (MidFTimes, PET, w3);
This uses ntrapz, the CMEX version of trapz, which has
the useful feature of allowing a weighting function to be supplied.
Thus, the first line of code above is equivalent to (but faster and
less memory-intensive than)
weight = ones (16384,1) * w1';
PETweighted = PET .* weight;
PET_int1 = trapz (MidFTimes, PETweighted');
- 9.
- Generate a simple mask based on PET_int1 (which is
simply the PET data averaged across all frames), and mask using
rescale. Also, mask is cleared for memory efficiency.
mask = PET_int1 > mean(PET_int1);
rescale (PET_int1, mask);
rescale (PET_int2, mask);
rescale (PET_int3, mask);
clear mask;
The next three steps perform delay/dispersion correction of the
blood data (see section 2.4).
- 10.
- First, create a mask that is used to select gray matter only;
the mask is a variation on that used to mask the weighted PET
integrals above. That is, simply select all voxels whose values are
greater than some constant times the mean of PET_int1. If
non-interactive mode is on (i.e. batch = 1, the default
behaviour), then this constant is hard-coded to 1.81; otherwise, the function
getmask is run. This allows the user to select the threshold
value while displaying the resulting, masked PET data.
if (batch)
mask = PET_int1 > (1.8*mean(PET_int1));
else
mask = getmask (PET_int1);
end
- 11.
- Use the mask to get the mean of all gray-matter voxels.
Thus, we reduce the dynamic PET data (16,384 voxels sampled at
n points in time) to a single time-activity curve (average of
gray-matter activity at n points in time).
A = (mean (PET (find(mask),:)))';
clear mask;
- 12.
- The actual delay/dispersion correction is performed by
correctblood. See sections 2.4, and
3.3.3 for information on (respectively) the
theoretical basis and the implementation of delay/dispersion
correction.
[ts_even, Ca_even, delta(:,current_slice)] = correctblood ...
(A, FrameTimes, FrameLengths, g_even, ts_even, progress);
- 13.
- Generate tables of the three weighted integrals of
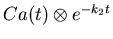 .
(Actually, we generate tables of this
expression integrated across each individual frame, then integrated
across all frames; the procedure is identical to that used in RCBF1
except for the addition of a third weighting function and the
greatly expanded range of possible values for k2.)
.
(Actually, we generate tables of this
expression integrated across each individual frame, then integrated
across all frames; the procedure is identical to that used in RCBF1
except for the addition of a third weighting function and the
greatly expanded range of possible values for k2.)
[conv_int1,conv_int2,conv_int3] = findintconvo (Ca_even,ts_even,...
k2_lookup, MidFTimes, FrameLengths, 1, w2, w3);
- 14.
- Generate some additional useful integrals. These are used more
than once in the subsequent code, and so are calculated in advance
to speed up the computation. Ca_mft is the blood data
averaged over each frame. This is taken as the value of the blood
data at the mid-frame time. Note that we must detect when the blood
data does not cover all the frames that the PET data does; this is
made easy because nframeint does the work for us. In
particular, if the start time of any frame (some element of
FrameTimes) is less than the start time of blood data
[ts_even(1)], then nframeint returns NaN
(not-a-number) in the element of Ca_mft corresponding to that
frame. Similarly, if the end time of any frame (some element of
FrameTimes+FrameLengths) is greater than the end time of
blood data [ts_even(length(ts_even))], then NaN
is also returned. The frames that fall outside of the blood data
are then not used in generating the weighted integrals of the blood data.
Ca_mft = nframeint (ts_even, Ca_even, FrameTimes, FrameLengths);
select = ~isnan(Ca_mft);
if (sum(select) ~= length(FrameTimes))
disp('Warning: blood data does not span frames.');
end
Ca_int1 = ntrapz(MidFTimes(select), Ca_mft(select), w1(select));
Ca_int2 = ntrapz(MidFTimes(select), Ca_mft(select), w2(select));
Ca_int3 = ntrapz(MidFTimes(select), Ca_mft(select), w3(select));
- 15.
- Generate the lookup table relating k2 to values of the right
hand side of equation (10). We also calculate the left
hand side of equation (10), which will be used in the
generation of a k2 image. Here, we see the value of precomputing
all the terms of rL and rR--not only is the code fairly
straightforward [as long as you understand the correspondence between
the variables Ca_inti, PET_inti and
conv_inti, and the terms of equation (10)],
but the computation of rL and rR is very fast.
Note that since PET_inti is an image (i.e. it contains
a value for each voxel in the slice), and Ca_inti is a
scalar, then rL will be an image. However,
conv_inti is a lookup table keyed on
k2_lookup; that is, there it contains one value for every
value of k2 presumed possible. Thus, rR will be also be a
lookup table keyed on k2_lookup.
rL = ((Ca_int3 * PET_int1) - (Ca_int1 * PET_int3)) ./ ...
((Ca_int3 * PET_int2) - (Ca_int2 * PET_int3));
rR = ((Ca_int3 * conv_int1) - (Ca_int1 * conv_int3)) ./ ...
((Ca_int3 * conv_int2) - (Ca_int2 * conv_int3));
- 16.
- Since rL and rR are the left- and right-hand-sides
of equation (10), we can use their equality to find
k2 for every voxel. That is, we know rL for every voxel,
and we know rR for a certain set of values of k2. Thus,
we can use rR to interpolate values of k2. First,
however, we must invert the current relationship between
k2_lookup and rR; that is, we must make
k2_lookup a lookup table keyed on the values of rR.
MATLAB's sort function makes this quite easy: we can sort
rR and get a vector containing the ``sort order'' in one
step. Since we need k2_lookup in its original order later
on, we make a copy called k2_sorted (even though it's now
scrambled) that is ordered according to rR.
[rR,sort_order] = sort (rR);
k2_sorted = k2_lookup (sort_order);
- 17.
- Generate the k2 image, through a simple table lookup.
Values of k2 are chosen by finding the value of k2 where
rL and rR are equal.
k2 = lookup(rR, k2_sorted, rL);
- 18.
- Generate the K1 image by evaluating the numerator of
equation (10). All of the time consuming calculations
have already been performed, and we can evaluate the
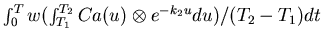 terms
through table lookup.
terms
through table lookup.
K1_numer = ((Ca_int3*PET_int1) - (Ca_int1 * PET_int3));
K1_denom = (Ca_int3 * lookup(k2_lookup,conv_int1,k2)) - ...
(Ca_int1 * lookup(k2_lookup,conv_int3,k2));
K1 = K1_numer ./ K1_denom;
- 19.
- Generate the V0 image by evaluating equation
(7) directly. Once again, we may get values for
the complicated part of the equation through simple table lookup.
V0 = (PET_int1 - (K1 .* lookup(k2_lookup,conv_int1,k2))) / Ca_int1;
- 20.
- Clean up the images by removing NaN's and infinities (setting
them to zero).
nuke = find (isnan (K1));
K1 (nuke) = zeros (size (nuke));
nuke = find (isinf (K1));
K1 (nuke) = zeros (size (nuke));
nuke = find (isnan (V0));
V0 (nuke) = zeros (size (nuke));
nuke = find (isinf (V0));
V0 (nuke) = zeros (size (nuke));
- 21.
- Convert from the units used internally to the standard units for
rCBF analysis.
rescale (K1, 100*60/1.05);
rescale (k2, 60);
rescale (V0, 100/1.05);
- 22.
- Finally, close the image file so that everything gets cleaned
up nicely.
closeimage (img);