function [new_ts_even, Ca_even, delta] = correctblood ...
(A, FrameTimes, FrameLengths, g_even, ts_even, options)
The input arguments are:
=
0=
- =-0.25in
0
=<: <879>>
- new_ts_even
- Generally the same as ts_even, with some elements possibly chopped off from the end due to shifting of the time scale.
- Ca_even
- g_even after correction for blood dispersion and delay.
- delta
- The computed delay correction
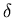 ,
in seconds.
,
in seconds.
- 2.
- Do the initial setup: calculate the mid-frame times, and find
frames that fall in the first 60 seconds of the study. (Although
the blood data is corrected over the entire study, the delay
correction is based on the PET data from the first 60 seconds only,
since the PET time-activity-curve is relatively flat by t=60.)
because
MidFTimes = FrameTimes + FrameLengths/2; first60 = find (FrameTimes < 60); % all frames in first numframes = length(FrameTimes); % minute only
- 3.
- Perform delay dispersion; we use deriv to compute a
smoothed version of g_even and its first derivative, and
then replace g_even with the dispersion-corrected
blood data (
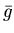 in equation 13).
in equation 13).
[smooth_g_even, deriv_g] = ... deriv (3, length(ts_even), g_even, (ts_even(2)-ts_even(1))); smooth_g_even(length(smooth_g_even)) = []; deriv_g(length(deriv_g)) = []; ts_even(length(smooth_g_even)) = []; g_even = smooth_g_even + tau*deriv_g; - 4.
- At this point, we are ready to start the delay
correction--i.e., we will find the value of
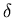 that gives a
function Ca (t) that best fits the PET activity A*(t) in
equation 12. However, there are three other
unknowns in equation 12, and it was found that a
full four-parameter fit was highly unstable. Therefore, we select a
fixed set of values for
that gives a
function Ca (t) that best fits the PET activity A*(t) in
equation 12. However, there are three other
unknowns in equation 12, and it was found that a
full four-parameter fit was highly unstable. Therefore, we select a
fixed set of values for 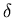 ,
perform multiple three-parameter
fits (for
,
perform multiple three-parameter
fits (for 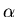 ,
,
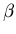 ,
and
,
and 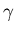 ), and select the value of
), and select the value of
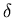 which resulted in the best fit.
which resulted in the best fit.
First, we prepare for the repeated fits. The fixed set of
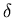 -values is selected; we initialize rss and
params (used to select the value of
-values is selected; we initialize rss and
params (used to select the value of 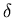 which resulted in
the best fit); and select values of
which resulted in
the best fit); and select values of 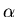 ,
,
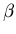 ,
and
,
and 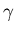 to start the fitting. These values are selected as being fairly
representative of real data
[
to start the fitting. These values are selected as being fairly
representative of real data
[
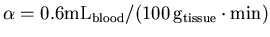 ,
,
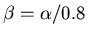 ,
and
,
and
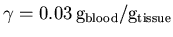 ],
but with
],
but with 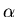 converted to our internal units of
converted to our internal units of
 and
and 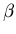 to 1/sec.
The init vector holds these values of
to 1/sec.
The init vector holds these values of 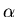 ,
,
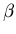 ,
and
,
and
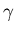 .
.
deltas = -5:1:10; init = [.0001 .000125 .03]; rss = zeros (length(deltas), 1); params = zeros (length(deltas), 3);
- 5.
- Now enter the loop through the values of
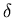 in
deltas. The first step is to copy the current element,
deltas(i), to delta; this is done solely to make the
code easier to read.
in
deltas. The first step is to copy the current element,
deltas(i), to delta; this is done solely to make the
code easier to read.
for i = 1:length(deltas) delta = deltas (i);
- 6.
- Now inside the loop, we perform a three-parameter fit for the
current value of
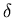 .
This is done by first computing
shifted_g_even, which is the current ``guess'' at Ca (t) (see equation 12). Note that the shifted
activity is computed from g_even, which at this point
contains
.
This is done by first computing
shifted_g_even, which is the current ``guess'' at Ca (t) (see equation 12). Note that the shifted
activity is computed from g_even, which at this point
contains
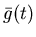 ,
the dispersion-corrected blood data (equation
13).
,
the dispersion-corrected blood data (equation
13).
shifted_g_even = lookup ((ts_even-delta), g_even, ts_even); g_select = find (~isnan (shifted_g_even));
- 7.
- Now perform the fit. The function delaycorrect
encapsulates the entire fitting procedure into one function; this is
equivalent to having one user-supplied function that evaluates the
function to minimize, and another function (such as fmins) to
iteratively evaluate and minimize this function. However, because
this method of delay correction was found to be extremely slow,
delaycorrect was written entirely in C as a special case.
final = delaycorrect (init, ... shifted_g_even(g_select), ... ts_even(g_select), ... A, FrameTimes, FrameLengths); - 8.
- Save the fit results (
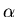 ,
,
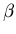 ,
and
,
and 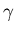 )
and
compute the residual (sum of the squares of the differences between
the data points and points on the fitted curve) for this value of
)
and
compute the residual (sum of the squares of the differences between
the data points and points on the fitted curve) for this value of
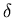 .
(fit_b_curve simply calls b_curve to
compute the right-hand-side of equation 11, the
``blood curve,'' for the current values of
.
(fit_b_curve simply calls b_curve to
compute the right-hand-side of equation 11, the
``blood curve,'' for the current values of 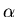 ,
,
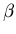 ,
,
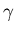 ,
and
,
and 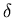 ,
at each mid-frame time. Then, it finds the
differences between this and the points on the PET activity curve
A, and returns the sum of the squares of these differences.
This is saved to the vector rss.
,
at each mid-frame time. Then, it finds the
differences between this and the points on the PET activity curve
A, and returns the sum of the squares of these differences.
This is saved to the vector rss.
params (i,:) = final; rss(i) = fit_b_curve (final, ... shifted_g_even(g_select), ts_even(g_select), ... A, FrameTimes, FrameLengths); - 9.
- Finally, we re-use the current values of
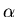 ,
,
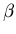 ,
,
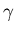 as initial values for the next fit and end the for loop.
as initial values for the next fit and end the for loop.
init = final; end % for delta
- 10.
- At this point, we have a vector of residual sums of squares (a single
number estimating the goodness-of-fit for each value of
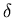 ).
To select the ``winning''
).
To select the ``winning''  ,
we simply find the minimum of
this vector.
,
we simply find the minimum of
this vector.
[err, where] = min (rss); delta = deltas (where);
- 11.
- Now that we have a value for delta, perform the actual
delay correction (shift the blood data). We must also remove NaN's
from the new data. These appear if lookup cannot perform a
lookup at a point (i.e., there is no corresponding point in the table).
They will therefore occur at the end points, where ts_even
does not span (ts_even-delta).
Ca_even = lookup ((ts_even-delta), g_even, ts_even); nuke = find(isnan(Ca_even)); Ca_even(nuke) = [];
- 12.
- And finally, make new_ts_even a truncated copy of
ts_even that fits Ca_even and reflects the loss of
information due to resampling at the very end of the data.
new_ts_even = ts_even; new_ts_even(nuke) = [];
Next: FINDINTCONVO Up: Annotated Program Listings Previous: RCBF2 Mark Wolforth <wolforth@bic.mni.mcgill.ca>
Greg Ward <greg@bic.mni.mcgill.ca>
Sean Marrett <sean@bic.mni.mcgill.ca>