<879>>=-0.25in
0
=<: <879>>
- Ca_even
- the blood data resampled at an evenly-spaced time
domain. Usually, this is as returned by resampleblood, and
possibly delay- and dispersion-corrected by correctblood.
- ts_even
- the time domain at which Ca_even was resampled.
- k2_lookup
- the list of k2 values at which to evaluate equation
![[*]](/icons/latex2html/cross_ref_motif.gif) . The output will consist of one value per
weighting function per value of k2.
. The output will consist of one value per
weighting function per value of k2.
- midftimes
- the mid-frame times (used to perform the
frame-by-frame integration).
- flengths
- the length of each frame (also used in the
frame-by-frame integration).
- w1,w2,w3
- the three weighting functions wi. w1 must be
supplied, but if it is an empty matrix, then a weighting function of
1 is assumed. w2 and w3 are not required, and if they
are not given, then int2 and int3 (respectively) will
not be defined in the output. Generally, the weighting funtions are
simple functions of t such as 1, t, or t2.
- progress
- an optional argument indicating whether progress should
be reported (in the form of printing a dot when the weighted
integrals for each value of k2 have been computed). This is
quite useful, as findintconvo is one of the most
time-consuming steps of RCBF analysis.
The output arguments int1, int2, and int3 are
simply vectors containing the value of equation 17 for
the three different weighting functions; each element of these vectors
corresponds to one value of k2 as supplied in k2_lookup.
- 2.
- Do some initial setup. We need to get the sizes of various
vectors, and initialize vectors that we will fill element by element
later. Initializing vectors to all zero before filling them allows
better memory management by MATLAB.
NumEvenTimes = length(ts_even);
NumFrames = length(midftimes);
fstart = midftimes - (flengths / 2);
TableSize = length (k2_lookup);
integrand = zeros (NumFrames, 1);
if (nargin >= 6); int1 = zeros (1, TableSize); end;
if (nargin >= 7); int2 = zeros (1, TableSize); end;
if (nargin == 8); int3 = zeros (1, TableSize); end;
% if w1 is empty, assume that it should be all ones
if isempty (w1)
w1 = ones (size(NumFrames));
end
- 3.
- Calculate each element of the integrals, one at a time.
Unfortunately, there does not seem to be any way to vectorize this
operation, and it must therefore be performed within an inefficient
for loop.
for i = 1:TableSize
- 4.
- First calculate the innermost terms of equation
17. exp_fun is
e-k2 t, and convo
is
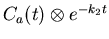 .
We then perform the inner
integration, i.e. average across all frames. This is performed by
nframeint, a special CMEX routine that has been carefully
optimised for this very common operation in RCBF analysis. Type
help nframeints in MATLAB for more information.
.
We then perform the inner
integration, i.e. average across all frames. This is performed by
nframeint, a special CMEX routine that has been carefully
optimised for this very common operation in RCBF analysis. Type
help nframeints in MATLAB for more information.
exp_fun = exp(-k2_lookup(i) * ts_even);
convo = nconv(Ca_even, exp_fun, ts_even(2) - ts_even(1));
integrand = nframeint (ts_even, convo(1:length(ts_even)),...
fstart, flengths);
- 5.
- Find any frames that are not completely covered by the
ts_even time domain. nframeint actually does this
for us, returning NaN (not-a-number) in any such element of its
output vector. Thus, we only use data from frames that are not equal to NaN, selected using the built-in isnan
function.
select = ~isnan(integrand);
- 6.
- Now we calculate the outer integral (the weighted integral
across all frames) for each weighting function with the current
value of k2. Again, we use a CMEX routine to enhance
performance; ntrapz is a replacement for MATLAB's
trapz function that is much faster, as well as having an
optional argument to allow weighting of the integrand. Note the use
of select to make sure that we only use frames actually
spanned by the blood data.
int1 (i) = ntrapz(midftimes(select), integrand(select), w1(select));
int2 (i) = ntrapz(midftimes(select), integrand(select), w2(select));
int3 (i) = ntrapz(midftimes(select), integrand(select), w3(select));
(We have omitted the code that makes w2 and w3
optional in favour of concentrating on the numerical analysis.)
- 7.
- End the for loop.
end
![\begin{displaymath}
\int_{0}^{T} \frac{\int\limits_{T_1}^{T_2}
\left[ C_{a}(u) \otimes e^{-k_{2}u} \right] du}{T_2 - T_1} \, w_i \, dt
\end{displaymath}](img45.gif)