Input and output arguments:
function integral = b_curve ...
(args, shifted_g_even, ts_even, A, fstart, flengths)
The output argument integral is just the values of equation
18 after frame-by-frame integration, i.e. there is one
number for each frame.
The input arguments are
=
0=
<879>>=-0.25in
0
=<: <879>>
- args
- a three element vector containing
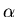 ,
,
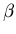 ,
and
,
and
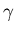 from equation
from equation ![[*]](/icons/latex2html/cross_ref_motif.gif) . Keep in mind in the
following code that args(1) is
. Keep in mind in the
following code that args(1) is 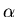 ,
args(1) is
,
args(1) is
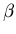 ,
and args(1) is
,
and args(1) is 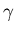 .
.
- g_even
- the blood data resampled at an evenly-spaced time
domain, and possibly shifted by some delay factor
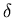 .
We
are not interested here in what that value of
.
We
are not interested here in what that value of 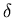 is,
however.
is,
however.
- ts_even
- the evenly-spaced time domain at which g_even
is sampled.
- A
- the PET activity, averaged over gray matter, for the current
slice. (This isn't actually used in b_curve, but the
argument is still here for historical reasons and to make calls
to b_curve and fit_b_curve look the same.)
- fstart
- the frame start times.
- flengths
- the frame lengths.
- 2.
- Evaluate the first term of the integrand in equation 18.
expthing = exp(-args(2)*ts_even);
c = nconv(shifted_g_even,expthing,ts_even(2)-ts_even(1));
c = c (1:length(ts_even));
i1 = args(1)*c; % alpha * (convolution)
- 3.
- Evaluate the second term of the integrand, and the two terms
together to get the integrand, i.
i2 = args(3)*shifted_g_even; % gamma * g(t - delta)
i = i1+i2;
- 4.
- Perform the frame-by-frame integration.
integral = nframeint (ts_even, i, fstart, flengths);
- 5.
- Clean up any NaN's that have cropped up by setting them to zero.
Also, truncate the function to whatever length A is.
nuke = find (isnan (integral));
integral (nuke) = zeros (size (nuke));
integral = integral (1:length(A));




Next: Using the rCBF Package
Up: Annotated Program Listings
Previous: FINDINTCONVO
Mark Wolforth
<wolforth@bic.mni.mcgill.ca>
Greg Ward
<greg@bic.mni.mcgill.ca>
Sean Marrett
<sean@bic.mni.mcgill.ca>
![\begin{displaymath}\frac{\int\limits_{T_1}^{T_2}
\left( \alpha
\left[ C_a(t)...
...e^{-\beta t} \right]
+ \gamma C_a(t) \right) dt} {T_2 - T_1}
\end{displaymath}](img48.gif)